las neuronas¶

"las neuronas"¶

# definimos la neurona, recibe de input un vector (x1,x2,...,xn)
# usa los pesos W (w1,w2,...,wn)
import numpy as np
def f(x, w):
# suma pesada
# sumo cada par xn*wn y al final el bias
# eso es el producto interno o dot product en algebra
wsum = np.dot(x,w[1:]) + w[0]
# activacion, si la suma pesada supera cierto limite la funcion
# tira un 1
# si no, tira un 0
if wsum >= 0.0:
output=1
else:
output=0
return output
import pandas as pd
dataset = [[2.7810836,2.550537003,0],
[1.465489372,2.362125076,0],
[3.396561688,4.400293529,0],
[1.38807019,1.850220317,0],
[3.06407232,3.005305973,0],
[7.627531214,2.759262235,1],
[5.332441248,2.088626775,1],
[6.922596716,1.77106367,1],
[8.675418651,-0.242068655,1],
[7.673756466,3.508563011,1]]
data=pd.DataFrame(dataset,columns=['x1','x2','y'])
data.head()
| x1 | x2 | y | |
|---|---|---|---|
| 0 | 2.781084 | 2.550537 | 0 |
| 1 | 1.465489 | 2.362125 | 0 |
| 2 | 3.396562 | 4.400294 | 0 |
| 3 | 1.388070 | 1.850220 | 0 |
| 4 | 3.064072 | 3.005306 | 0 |
X=data[['x1','x2']]
y=data.y
# veamos como funciona si los pesos ya nos vienen definidos
# un peso por cada xn y un bias (3)
weights = np.array([5, -91, 91])
# miro el output de mi neurona para cada fila
# comparo con la columna 'y' el target
for i,x in enumerate(X.values):
prediction = f(x, weights)
print("Target=%d, Prediccion=%d" % (y[i], prediction))
Target=0, Prediccion=0 Target=0, Prediccion=1 Target=0, Prediccion=1 Target=0, Prediccion=1 Target=0, Prediccion=0 Target=1, Prediccion=0 Target=1, Prediccion=0 Target=1, Prediccion=0 Target=1, Prediccion=0 Target=1, Prediccion=0
# veamos como funciona si los pesos ya nos vienen definidos
# un peso por cada xn y un bias (3)
weights = np.array([-0.1, 0.20653640140000007, -0.23418117710000003])
# miro el output de mi neurona para cada fila
# comparo con la columna 'y' el target
for i,x in enumerate(X.values):
prediction = f(x, weights)
print("Target=%d, Prediccion=%d" % (y[i], prediction))
Target=0, Prediccion=0 Target=0, Prediccion=0 Target=0, Prediccion=0 Target=0, Prediccion=0 Target=0, Prediccion=0 Target=1, Prediccion=1 Target=1, Prediccion=1 Target=1, Prediccion=1 Target=1, Prediccion=1 Target=1, Prediccion=1
# Pero como obtengo los parametros/pesos y biases?
# Como obtenia los betas/parametros de cualquier modelo?
# descenso gradiente!
def train_weights(x_train,y_train, l_rate, n_epoch):
#inicio con w = 0,0...0
weights = [0.0 for i in range(len(x_train[0])+1)]
print('>epoch=-1, lrate=%.3f, error=inf,w0=%.3f, w1=%.3f, w2=%.3f' %(l_rate,weights[0], weights[1], weights[2]))
#itero
for epoch in range(n_epoch):
sum_error = 0.0
#predigo sobre las filas
for i,x in enumerate(x_train):
prediction = f(x, weights)
# calculo la funcion de costo
error = y_train[i] - prediction
sum_error += error**2
# defino los nuevos pesos en la direccion del gradiente
# l_rate era la longuitud del paso en esa direccion
weights[0] = weights[0] + l_rate * error
for i in range(len(x)):
weights[i + 1] = weights[i + 1] + l_rate * error * x[i]
print('>epoch=%d, lrate=%.3f, error=%.3f, w0=%.3f, w1=%.3f, w2=%.3f' %
(epoch, l_rate, sum_error, weights[0], weights[1], weights[2]))
return weights
# ahora si, entrenemos nuestra neurona
l_rate = 0.1
n_epoch = 5
weights = train_weights(X.values,y, l_rate, n_epoch)
>epoch=-1, lrate=0.100, error=inf,w0=0.000, w1=0.000, w2=0.000 >epoch=0, lrate=0.100, error=2.000, w0=0.000, w1=0.485, w2=0.021 >epoch=1, lrate=0.100, error=1.000, w0=-0.100, w1=0.207, w2=-0.234 >epoch=2, lrate=0.100, error=0.000, w0=-0.100, w1=0.207, w2=-0.234 >epoch=3, lrate=0.100, error=0.000, w0=-0.100, w1=0.207, w2=-0.234 >epoch=4, lrate=0.100, error=0.000, w0=-0.100, w1=0.207, w2=-0.234
for i,x in enumerate(X.values):
prediction = f(x, weights)
print("Target=%d, Prediccion=%d" % (y[i], prediction))
Target=0, Prediccion=0 Target=0, Prediccion=0 Target=0, Prediccion=0 Target=0, Prediccion=0 Target=0, Prediccion=0 Target=1, Prediccion=1 Target=1, Prediccion=1 Target=1, Prediccion=1 Target=1, Prediccion=1 Target=1, Prediccion=1
weights
[-0.1, 0.20653640140000007, -0.23418117710000003]
Veamos como funciona¶
Tomemos un x (una fila)
x
array([7.67375647, 3.50856301])
f(x, weights)
1
No es una regresion logistica con sombrero nuevo?¶
Un modelo que era una combinacion lineal de las features que tiraba 0 y 1....
"la neurona"¶

Activacion¶
Que hace que no sea una simple combinacion lineal del input?
Nonlinear functions¶
- (a) Sigmoid function
- (b) Tanh function
- (c) ReLU function
- (d) Leaky ReLU function.
Se puede demostrar que sin la no linealidad de la funcion de activacion, cualquier red neuronal por mas compleja que sea se puede reducir a una red de una sola capa con coeficientes lineales.
Por que Deep Learning?¶
En teoria una red neuronal de una sola capa con muchas neuronas, podria aproximar cualquier funcion, pero es mas eficiente entrenar una red de varias capaz de tamaño reducido.
Como controlamos la complejidad (capacidad de aprendizaje) de una red?
- Numero de Neuronas (width).
- Numero de Layers (depth).

...Theoretical results strongly suggest that in order to learn the kind of complicated functions that can represent high-level abstractions (e.g. in vision, language, and other AI-level tasks), one needs deep architectures. Deep architectures are composed of multiple levels of non-linear operations, such as in neural nets
with many hidden layers... - Yoshua Bengio (2009), "Learning Deep Architectures for AI"- Deeper redes permiten usar menos parametros, las shallow redes no son buenas para abstraer conocimiento (reducir la dimensionalidad) https://arxiv.org/pdf/1312.6098.pdf

Relational and semantic knowledge can be obtained at higher levels of abstraction and representation of the raw data (Yoshua Bengio and Yann LeCun, Scaling Learning Algorithms towards AI, 2007).
Deep architectures can be representationally efficient. This sounds contradictory, but its a great benefit because of the distributed representation power by deep learning.
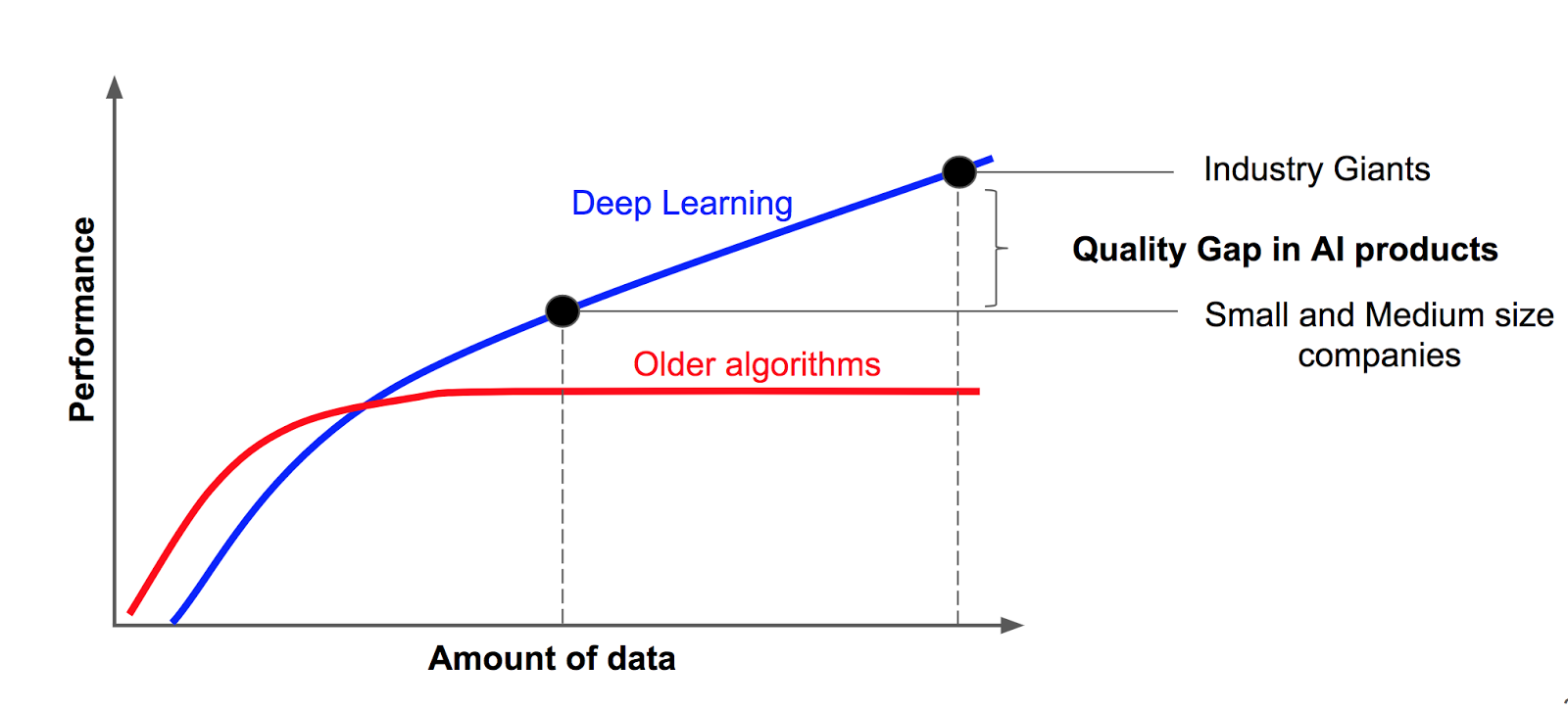
- The learning capacity of deep learning algorithms is proportional to the size of data, that is, performance increases as the input data increases, whereas, for shallow or traditional learning algorithms, the performance reaches a plateau after a certain amount of data is provided as shown in the following figure, Learning capability of deep learning versus traditional machine learning:



Como encuentro los betas?¶
Como siempre...minimizo la funcion de costo. Si quiero entrenar mi red para clasificar perro/gato uso las mismas metricas de la toda la vida para ajustar los betas de la ultima capa que decide si es perro o gato. Derivo la funcion de costo... funcion que depende de los betas de la ultima capa, la anterior, la antepenultima y asi...
Backpropagation es solo la regla de la cadena*¶

Pero una red neuronal tiene una forma analitica cerrada que podemos derivar?
Veamos que pinta tiene una funcion de costo:

Optimizadores¶
Como vimos en el curso para buscar el minimo de la funcion de costo no derivamos, iteramos (epochs) con pasitos cortos (learning rate) en la direccion de mayor pendiente en busqueda del minimo.
Adaptative Learning Rates¶
Algoritmos que van regulando el learning rate para optimizar la busqueda.
Batched Stochastic Gradient Descent¶
SGD de siempre calculado en pedazos (batches) random del training set.
Regularizacion (evitando el overfitting)¶
Data augmentation¶
Se perturban los datos para evitar el overfiting (la misma foto del perrito, rotada, flipeada, cropeada, etc)
Dropout¶
De manera aleatoria matamos neuronas con una birrita en cada iteracion, obligamos a que todas las neuronas aprendan. Esto hace que la red sea robusta y que pueda generalizar.
Early Stopping¶
Dejamos de iterar cuando en un set de cross validation empezamos a performar mal.
Redes Multicapa¶
Veamos un ejemplo de como construir una red neuronal para el dataset de los digitos escritos a mano:
El objetivo es una funcion (red neuronal) que tome como input la imagen de un numero (por ejemplo el 8) y su output un vector de 10 dimensiones con las probabilidades de pertenencia a cada clase.

Estructura de la Red¶
network = [
FlattenLayer(input_shape=(28, 28)),
FCLayer(28 * 28, 20),
ActivationLayer(relu, relu_prime),
FCLayer(20, 10),
SoftmaxLayer(10)
]- 28*28 pixeles tienen las imagenes, la primer capa vectoriza las imagenes
- la segunda capa tiene 20 'neuronas' (20 combinaciones lineales de las 28*28 variables)
- la capa de activacion donde meto la no linealidad
- una tercer capa que conecta 20 neuronas con las 10 neuronas finales (una por cada clase)
- la ultima capa solo se encarga de normalizar la salida para obtener las probabilidades
Vamos a definir cada capa como una clase, una clase era una 'funcion' que podia tener funciones y variables embebidas. Durante todo el curso usamos objetos clase cuando usabamos un modelo, modelo.fit, etc.
# reshapea el input
class FlattenLayer:
def __init__(self, input_shape):
self.input_shape = input_shape
def forward(self, input):
return np.reshape(input, (1, -1))
# capa fully conected
class FCLayer:
def __init__(self, input_size, output_size):
self.input_size = input_size
self.output_size = output_size
self.weights = np.random.randn(input_size, output_size) / np.sqrt(input_size + output_size)
self.bias = np.random.randn(1, output_size) / np.sqrt(input_size + output_size)
def forward(self, input):
self.input = input
return np.dot(input, self.weights) + self.bias
# activacion (no linealidad)
class ActivationLayer:
def __init__(self, activation, activation_prime):
self.activation = activation
self.activation_prime = activation_prime
def forward(self, input):
self.input = input
return self.activation(input)
# reshapea el output, normaliza sobre la cantidad de clases
class SoftmaxLayer:
def __init__(self, input_size):
self.input_size = input_size
def forward(self, input):
self.input = input
tmp = np.exp(input)
self.output = tmp / np.sum(tmp)
return self.output
Y el descenso grandiente?¶
# reshapea el input
class FlattenLayer:
def __init__(self, input_shape):
self.input_shape = input_shape
def forward(self, input):
return np.reshape(input, (1, -1))
def backward(self, output_error, learning_rate):
return np.reshape(output_error, self.input_shape)
# capa fully conected
class FCLayer:
def __init__(self, input_size, output_size):
self.input_size = input_size
self.output_size = output_size
self.weights = np.random.randn(input_size, output_size) / np.sqrt(input_size + output_size)
self.bias = np.random.randn(1, output_size) / np.sqrt(input_size + output_size)
def forward(self, input):
self.input = input
return np.dot(input, self.weights) + self.bias
def backward(self, output_error, learning_rate):
input_error = np.dot(output_error, self.weights.T)
weights_error = np.dot(self.input.T, output_error)
# bias_error = output_error
self.weights -= learning_rate * weights_error
self.bias -= learning_rate * output_error
return input_error
# activacion (no linealidad)
class ActivationLayer:
def __init__(self, activation, activation_prime):
self.activation = activation
self.activation_prime = activation_prime
def forward(self, input):
self.input = input
return self.activation(input)
def backward(self, output_error, learning_rate):
return output_error * self.activation_prime(self.input)
# reshapea el output, normaliza sobre la cantidad de clases
class SoftmaxLayer:
def __init__(self, input_size):
self.input_size = input_size
def forward(self, input):
self.input = input
tmp = np.exp(input)
self.output = tmp / np.sum(tmp)
return self.output
def backward(self, output_error, learning_rate):
input_error = np.zeros(output_error.shape)
out = np.tile(self.output.T, self.input_size)
return self.output * np.dot(output_error, np.identity(self.input_size) - out)
# importamos los datos
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float32')
x_train /= 255
y_train = np_utils.to_categorical(y_train)
x_train = x_train[0:1000]
y_train = y_train[0:1000]
x_test = x_test.astype('float32')
x_test /= 255
y_test = np_utils.to_categorical(y_test)
network = [
FlattenLayer(input_shape=(28, 28)),
FCLayer(28 * 28, 20),
ActivationLayer(relu, relu_prime),
FCLayer(20, 10),
SoftmaxLayer(10)
]
def train(network,x_train, y_train, epochs=40,learning_rate=0.1):
err=[]
# training
for epoch in range(epochs):
error = 0
for x, y_true in zip(x_train, y_train):
# forward
output = x
for layer in network:
output = layer.forward(output)
# error (display purpose only)
error += mse(y_true, output)
# backward
output_error = mse_prime(y_true, output)
for layer in reversed(network):
output_error = layer.backward(output_error, learning_rate)
error /= len(x_train)
err.append(error)
return(network,err)
def predict(network, input):
output = input
for layer in network:
output = layer.forward(output)
return output
network,err=train(network,x_train,y_train)
plt.plot(err)
plt.grid(True)
plt.ylabel('error')
plt.xlabel('epochs')
plt.show()
# veamos la performance en el set de testeo
accuracy = sum([np.argmax(y) == np.argmax(predict(network, x)) for x, y in zip(x_test, y_test)]) / len(x_test)
error = sum([mse(y, predict(network, x)) for x, y in zip(x_test, y_test)]) / len(x_test)
print('accuracy: %.4f' % accuracy)
print('mse: %.4f' % error)
accuracy: 0.8592 mse: 0.0214
Hay que hacer todo eso a mano?¶
TensorFlow¶
Libreria de google para redes neuronales, antiguamente se usaba una libreria aparte llamada KERAS para armar las redes, hoy keras esta incluida en TF.
Esta es la arquitectura de nuestra red:
network = [
FlattenLayer(input_shape=(28, 28)),
FCLayer(28 * 28, 20),
ActivationLayer(relu, relu_prime),
FCLayer(20, 10),
SoftmaxLayer(10)
]Como implementamos esto en Tf?
import tensorflow as tf
import tensorflow.keras as ks
model = ks.models.Sequential()
model.add(ks.layers.Flatten(input_shape=(28, 28)))
model.add(ks.layers.Dense(20,activation=tf.nn.relu))
model.add(ks.layers.Dense(20,activation=tf.nn.relu))
model.add(ks.layers.Dense(10,activation=tf.nn.softmax))
model.compile(
loss='categorical_crossentropy',
metrics=['accuracy']
)
Metal device set to: Apple M1
2022-01-05 11:49:59.680588: I tensorflow/core/common_runtime/pluggable_device/pluggable_device_factory.cc:305] Could not identify NUMA node of platform GPU ID 0, defaulting to 0. Your kernel may not have been built with NUMA support. 2022-01-05 11:49:59.681753: I tensorflow/core/common_runtime/pluggable_device/pluggable_device_factory.cc:271] Created TensorFlow device (/job:localhost/replica:0/task:0/device:GPU:0 with 0 MB memory) -> physical PluggableDevice (device: 0, name: METAL, pci bus id: <undefined>)
model.fit(x_train,y_train,epochs=10);
2022-01-05 11:50:09.582022: I tensorflow/compiler/mlir/mlir_graph_optimization_pass.cc:185] None of the MLIR Optimization Passes are enabled (registered 2) 2022-01-05 11:50:09.585347: W tensorflow/core/platform/profile_utils/cpu_utils.cc:128] Failed to get CPU frequency: 0 Hz 2022-01-05 11:50:09.732770: I tensorflow/core/grappler/optimizers/custom_graph_optimizer_registry.cc:112] Plugin optimizer for device_type GPU is enabled.
Epoch 1/10 32/32 [==============================] - 0s 6ms/step - loss: 2.0896 - accuracy: 0.3070 Epoch 2/10 32/32 [==============================] - 0s 6ms/step - loss: 1.6577 - accuracy: 0.5780 Epoch 3/10 32/32 [==============================] - 0s 6ms/step - loss: 1.2963 - accuracy: 0.7120 Epoch 4/10 32/32 [==============================] - 0s 6ms/step - loss: 0.9988 - accuracy: 0.7720 Epoch 5/10 32/32 [==============================] - 0s 7ms/step - loss: 0.7726 - accuracy: 0.8220 Epoch 6/10 32/32 [==============================] - 0s 6ms/step - loss: 0.6278 - accuracy: 0.8490 Epoch 7/10 32/32 [==============================] - 0s 6ms/step - loss: 0.5279 - accuracy: 0.8650 Epoch 8/10 32/32 [==============================] - 0s 7ms/step - loss: 0.4518 - accuracy: 0.8850 Epoch 9/10 32/32 [==============================] - 0s 7ms/step - loss: 0.3957 - accuracy: 0.8950 Epoch 10/10 32/32 [==============================] - 0s 7ms/step - loss: 0.3547 - accuracy: 0.9070
Veamos como nos fue en el test:¶
val_loss,val_acc = model.evaluate(x_test,y_test)
print("loss-> ",val_loss,"\nacc-> ",val_acc)
37/313 [==>...........................] - ETA: 1s - loss: 0.6280 - accuracy: 0.8041
2022-01-05 11:50:39.785266: I tensorflow/core/grappler/optimizers/custom_graph_optimizer_registry.cc:112] Plugin optimizer for device_type GPU is enabled.
313/313 [==============================] - 1s 4ms/step - loss: 0.5606 - accuracy: 0.8291 loss-> 0.5605828166007996 acc-> 0.8291000127792358
Miremos una sola prediccion:¶
predictions=model.predict([x_test])
predictions[0]
2022-01-05 13:28:45.429811: I tensorflow/core/grappler/optimizers/custom_graph_optimizer_registry.cc:112] Plugin optimizer for device_type GPU is enabled.
array([6.1261046e-05, 4.9726212e-05, 5.9080147e-04, 4.1295623e-04,
1.6288496e-04, 1.8081400e-05, 3.3151041e-04, 9.9380589e-01,
1.1645434e-04, 4.4504441e-03], dtype=float32)
y_test[0]
array([0., 0., 0., 0., 0., 0., 0., 1., 0., 0.], dtype=float32)
print('label -> ',np.argmax(y_test[2]))
print('prediction -> ',np.argmax(predictions[2]))
label -> 1 prediction -> 1
print('label -> ',np.argmax(y_test[20]))
print('prediction -> ',np.argmax(predictions[20]))
label -> 9 prediction -> 9
plot(sample(aciertos,12))
plot(sample(errores,12))
Cuando usar deep learning? tiramos todo lo que aprendimos en el curso?¶
Miremos la performance de una NN en uno de los dataset que usamos en el curso, como el de 'hitter.csv' si, ese, malisimo! Ya se, pero bueno es uno de los que mas usamos (263 jugadores, 19 variables)
Ajustamos esos datos con una regresion lineal, lasso y una NN. Aca los resultados:

No solo no performo mejor que una regresion comun, si no que ademas tiene 1.4k parametros!
Donde si usar deep learning:¶
+ cv (img+video)
+ generative learning
+ nlp
+ audio
+ reinforcement learning (rl)cv¶
Image Classification:¶


Instance Segmentation:¶
detect objects and associate each pixel inside object area with an instance label.

Superesolution y superfluidez¶

YouTubeVideo('Fxd8XJ_J0Gc', width=720, height=405)
generative deep learning¶
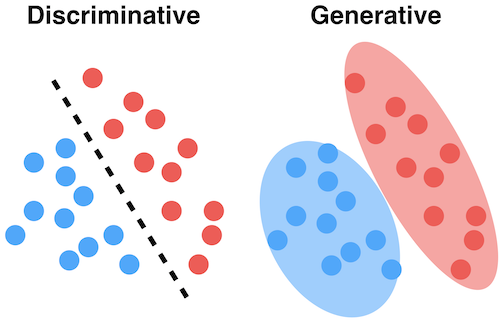


GANs¶

YouTubeVideo('cQ54GDm1eL0', width=720, height=405)
deepfakes¶

YouTubeVideo('HG_NZpkttXE?t=99', width=720, height=405)
nlp¶


text summarization¶

img+nlp¶

input: 'deep learning'

~vqgan+clipYouTubeVideo('VNrmG4EvFs8', width=720, height=405)
reinforcement learning¶


Links¶
nlp+cv¶
https://openai.com/blog/image-gpt/
https://openai.com/blog/dall-e/